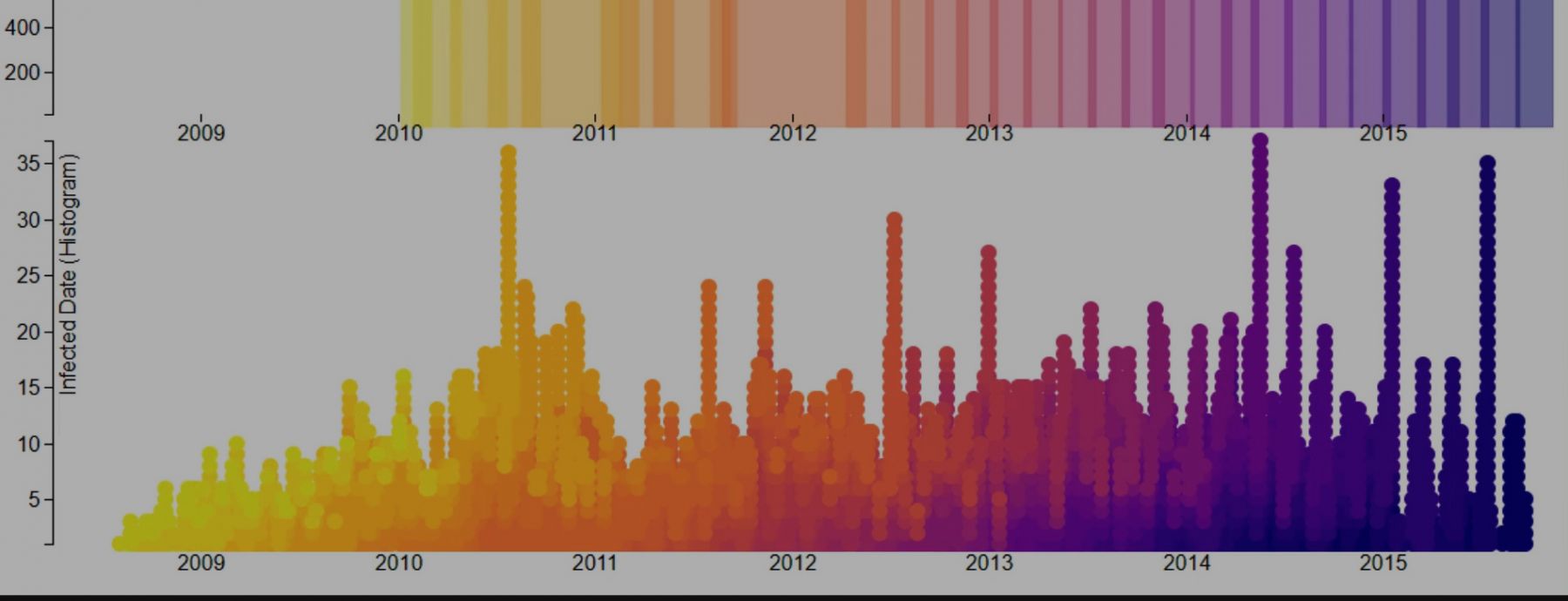
Center Overview
CIDD encompasses expertise in such basic fields as ecology, evolution, mathematical biology and molecular biology as well as applied disciplines including epidemiology, drug development, and vector control. We have partnerships across the globe with academic institutions, health agencies, and industry leaders to help bring its science into translational practice. Trainees in CIDD benefit from developing scientifically in this rich collaborative research environment, informed and shaped by real world practice.